What are trapped Rydberg ions?
Rydberg ions are orders of magnitude bigger than normal ions. They possess an outermost electron which resides in highly excited orbitals far away from the atomic core. The highly excited electron is almost not trapped anymore. The picture below demonstrates the dimension of a Rydberg ion with respect to other important dimensions in an ion trap. The size of a Rydberg ion can be bigger than its localization inside the trap, but will still be smaller than the typical ion-ion distance. The resulting physical properties make trapped Rydberg ions a promising system for quantum information processing. For instance, due to their size they are able to sense other Rydberg ions across distances of several micrometers which enables fast quantum operations.
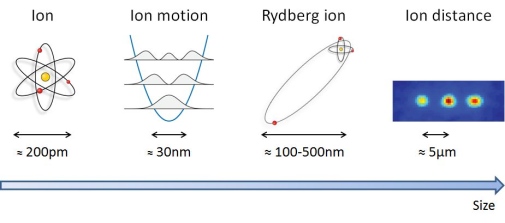
What makes trapped Rydberg ions special?
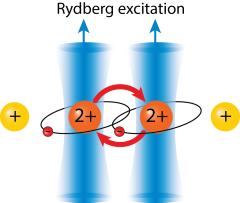
Trapped Rydberg ions can form very large dipoles. For example, a microwave field driving transitions between Rydberg states can induce large oscillating dipoles. For the Rydberg state with quantum number n=65 the oscillating dipole moment can reach up to 10000 Debye, while a diatomic molecule has typically 10 Debye and the quantum oscillation of an ion in the trap usually is about 300 Debye (in SI units: 1 Debye = 3.3×10−30 Cm). Two oscillating dipoles next to each other can repel or attract each other. Neighboring Rydberg ions with large oscillating dipoles will therefore sense each other more strongly than this is the case for two oscillating ions.
How to make trapped Rydberg ions?
Ions are trapped by static and oscillating electric fields. Coulomb repulsion of the charged particles results in a linear chain of ions separated by 5µm. This separation allows each ion to be individually addressed by laser beams. The electronic state of the ion can be used to store quantum bits (qubits): for instance the electronic ground state S1/2 can be defined as state 1, and the metastable state D5/2 as state 0. Single qubit rotations are carried out by driving the electronic transition with a laser.

We generate Rydberg ions by exciting a normal trapped ion into the Rydberg state. A laser brings the outermost electron from the ground state into the Rydberg state. Unfortunately, for ions the outermost electron is were tightly bound so that it takes a lot of energy to induce the transition from the ground state to the Rydberg state. For example, for strontium ions this requires a laser with a wavelength of 112.4nm. Such ultraviolet light is very difficult to generate and is immediately absorbed by air. We therefore chose to use two lasers where the first laser excites an intermediate state (wavelength of 242.6nm from 4D5/2 to 6P3/2) before the second laser finally reaches the Rydberg states (wavelength 304-309nm from 6P3/2 to nS or nD Rydberg states with n=30-infinity).
What have we done?
In the last few years we have demonstated that Rydberg ions are indeed a useful quantum technology. In 2017, we reported on the excitation of a single trapped strontium ion into the Rydberg state [1]. In this work we investigated the physical properties of Rydberg states due to the interaction with the trapping field. In the same year we carried out the first coherent Rydberg excitation of an ion and perform a single-qubit Rydberg gate, thus demonstrating basic elements of a trapped Rydberg ion quantum computer [2]. Both publications are part of Gerard Higgins' PhD thesis [3]. In 2019, we then excite a trapped ion to a Rydberg state with polarizability ∼8 orders of magnitude higher than a low-lying electronic state. We found that the highly polarizable ion experiences a vastly different trapping potential owing to the Stark effect [4]. We observed changes in trap stiffness, equilibrium position, and minimum potential, which can be tuned using the trapping electric fields.
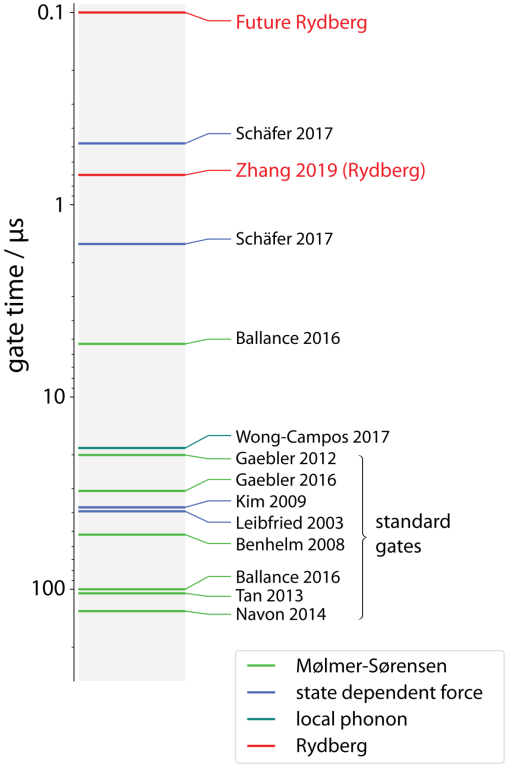
The goal of this project is to speed up trapped ion entangling operations via Rydberg interaction. Recently, we have demonstrated a sub-microsecond entangling gate between two ions via dipolar Rydberg interaction [5]. This marks a 50-fold speedup of quantum gate operations compared to standard motion-based quantum operations in trapped ions (see Fig. 4). Notably the gate speed depends on the ion distance and a further 10-fold improvement in gate speed seems realistic for longer ion strings. The future goal of this project is to operate ultra-fast quantum calculations in larger crystals of trapped Rydberg ions.

Project members
Former members
- Andreas Pöschl
- Christine Maier
- Florian Kress
- Guillaume Coppola
- Johannes Haag
- Quentin Bodart
[1] Single Strontium Rydberg Ion Confined in a Paul Trap
G. Higgins, W. Li, F. Pokorny, C. Zhang, F. Kress, C. Maier, J. Haag, Q. Bodart, I. Lesanovsky, M. Hennrich
Phys. Rev. X 7, 021038 (2017), arXiv:1611.02184.
[2] Coherent Control of a Single Trapped Rydberg Ion
Gerard Higgins, Fabian Pokorny, Chi Zhang, Quentin Bodart, and Markus Hennrich
Phys. Rev. Lett. 119, 220501 (2017), arXiv:1708.06387.
[3] A Single Trapped Rydberg Ion
Gerard Higgins
PhD thesis (2018) Stockholm University and University of Innsbruck as cotutelle PhD.
Selected for the Springer thesis award as outstanding PhD thesis from around the world and across the physical sciences.
Download here on Diva and at Springer.
[4] Highly-polarizable Rydberg ion in a Paul trap
G. Higgins, F. Pokorny, C. Zhang, and M. Hennrich
Phys. Rev. Lett. 123, 153602 (2019), arXiv:1904.08099.
[5] Sub-microsecond entangling gate between trapped ions via Rydberg interaction
Chi Zhang, Fabian Pokorny, Weibin Li, Gerard Higgins, Andreas Pöschl, Igor Lesanovsky, Markus Hennrich
arXiv:1908.11284.





